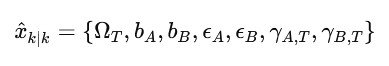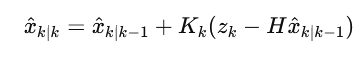What if we could demonstrate the Earth’s rotation using nothing more than a simple microcontroller, two MEMS gyroscopes, and a bit of algorithmic ingenuity? In this article, I present a device that makes it possible to locally measure the Earth’s rotation rate using only “off-the-shelf” gyroscopes—in this case, BMI160 sensors.

The appeal of this approach is both experimental and related to signal processing. One motivation for the project actually comes from a conversation with a neighbor—who, as it turns out, is a flat-earther. I have nothing against questioning established ideas; I even like to think of myself as open-minded, and it seems healthy to doubt things—after all, that’s the foundation of the scientific method. But in this particular case, the argument becomes downright absurd. Among other questionable claims, he insisted that it is impossible to locally measure the Earth’s rotation rate.

I show that it is indeed possible to locally measure the Earth’s rotation rate, by combining two Bosch BMI160 MEMS gyroscopes, a Pi Pico microcontroller, a motorized turntable (NEMA17), and advanced signal processing techniques: dithering, controlled rotation of the sensor, and Kalman filtering to fuse the measurements from both sensors and from different positions. The precision achieved (on the order of one percent) matches the theoretical value.

Why is this not trivial?

The Earth completes a full turn in 23 h 56 min 4 s (sidereal day), i.e., 0.00416 °/s. Detecting such a low speed with MEMS gyroscopes is not straightforward: at ± 125 °/s, the BMI160 outputs 262.4 LSB/°/s, which puts the LSB around 0.0038 °/s—the Earth’s rotation is barely more than a single bit of raw resolution. At first glance, it would seem impossible to make this measurement with such sensors.

The core of the method

Two key strategies make it possible:

1. Taking a huge number of measurements: literally hundreds of thousands of data points are collected.
   If the sensor noise is “white,” the variance decreases as 1/n and the standard deviation as 1/√n.

2. Moving the sensor during measurement, in order to identify the bias of each gyroscope and the influence of gravitational acceleration on the measurement.

Concretely, both of these aspects are handled in a Kalman filter, which processes the measurements from the four tested positions for the pair of sensors.
The goal is to identify a rotation rate that is constant—even if very weak. The entire acquisition chain is designed to isolate this constant while minimizing the influence of sensor biases and dependencies on temperature or gravitational acceleration.

The four positions

While the method would work with a single sensor, using two doubles the acquisition bandwidth, which speeds up obtaining a statistically robust measurement.

Before each measurement, the setup is oriented toward the north. The sensor then rotates about a horizontal axis perpendicular to the north-south direction.

It is moved through four positions during an acquisition cycle (look at the video):

• Position 1: sensor aligned with the Earth’s rotation axis (90° – azimuth relative to the horizontal, facing north). One cycle consists of 128 readings (32 per position, 16 per sensor), lasting about 10 seconds.

• Position 2: rotated 180° from position 1.

• Position 3: a further 90° rotation.

• Position 4: another 180° rotation from position 3 (i.e., 270° from position 1).

The measurement equations are as follows:

At Position 1:

θP1,A = ΩT + bA + ϵA·TA + nA,T + (g⋅n_measure)·γA,T
θP1,B = –ΩT + bB + ϵB·TB + nB,T – (g⋅n_measure)·γB,T

Position 2 (180°):

θP2,A = –ΩT + bA + ϵA·TA + nA,T + (g⋅n_measure)·γA,T
θP2,B = ΩT + bB + ϵB·TB + nB,T – (g⋅n_measure)·γB,T

Positions 3 (90°) and 4 (270°):

θP3,A = bA + ϵA·TA + nA,T + (g⋅n_measure)·γA,T
θP3,B = bB + ϵB·TB + nB,T – (g⋅n_measure)·γB,T

θP4,A = bA + ϵA·TA + nA,T + (g⋅n_measure)·γA,T
θP4,B = bB + ϵB·TB + nB,T – (g⋅n_measure)·γB,T

Where:

• ΩT: Earth’s rotation rate

• bA, bB: bias of sensors A and B

• ϵA, ϵB: temperature sensitivity coefficients

• TA, TB: temperatures of sensors

• nA,T, nB,T: measurement noise

• (g⋅n_measure): projection of gravity along the measurement axis

• γA,T, γB,T: coefficients for gravity influence

By intelligently combining the measurements from the different positions—for example, by subtracting the measurement in position 2 from that in position 1—it is possible to separate the signal of interest (the Earth’s rotation) from noise and systematic biases: the rotation term changes sign, while the biases and certain disturbances remain constant or vary differently.
This trick is effective provided the measurement and rotation times are short compared to the characteristic time over which sensor bias drifts; in other words, the biases must remain approximately constant during the entire measurement cycle.
In practice, one could already obtain a reasonable estimate of the Earth’s rotation using only these differences. However, it is much more effective to fully fuse all the measurements via a Kalman filter, which optimally extracts the signal in the presence of noise, bias, and various fluctuations.

Kalman filter

Even on a microcontroller like the Pi Pico, it is possible to run a Kalman filter with only a handful of parameters. Integrating the experimental results for each 4-position cycle (about 10 seconds) takes around 1.5 seconds of processing time.

State estimation

The essential state variables are:

• ΩT: Earth’s rotation rate

• bA, bB: biases specific to each sensor

• ϵA, ϵB: temperature sensitivity coefficients

• γA,T, γB,T: coefficients for gravity influence

These variables are estimated using the Kalman filter, which allows the relevant information to be extracted even in the presence of noise and uncertainty.

The filter follows the standard update equation:

• xk|k : state estimate at instant k after update

• Kk : Kalman gain

• zk: vector of measurements

• $H$: observation matrix defined by the above model

  

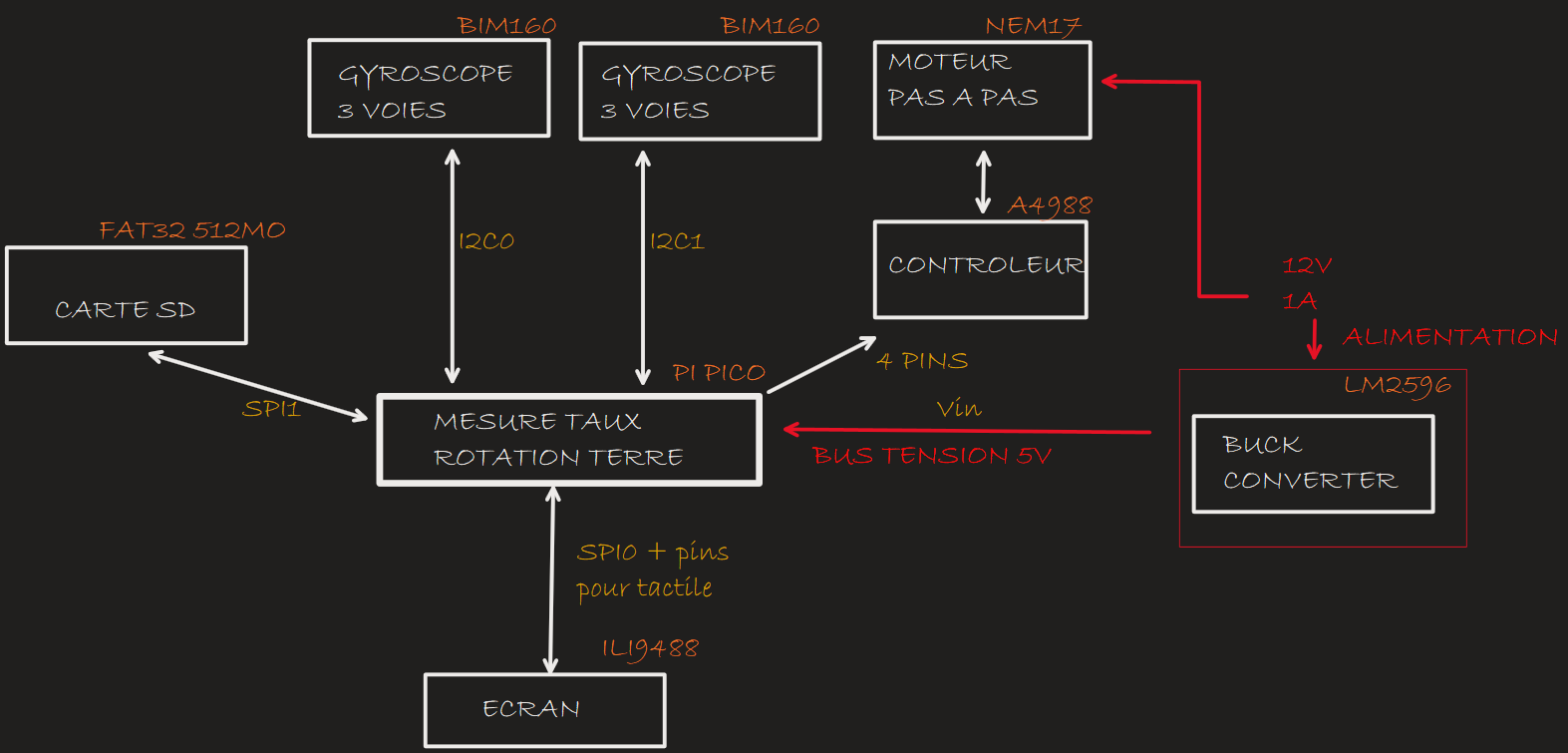
Experimental setup

The setup includes:

• a NEMA17 motor and a turntable providing controlled rotation of the two sensors

• a custom PCB with an A9488 driver to control the motor

• a display (ILI9488 controller) for real-time visualization (SPI0)

• an SD card on the second SPI port

• two BMI160 gyroscopes (widely used, inexpensive MEMS)

The operation of these MEMS sensors is fascinating: they measure the deflection of a vibrating beam, linked to the Coriolis effect, which ultimately means measuring a deformation of just a few ångströms! And yet, the Earth moves—and we can detect it!

Experimental results and conclusion

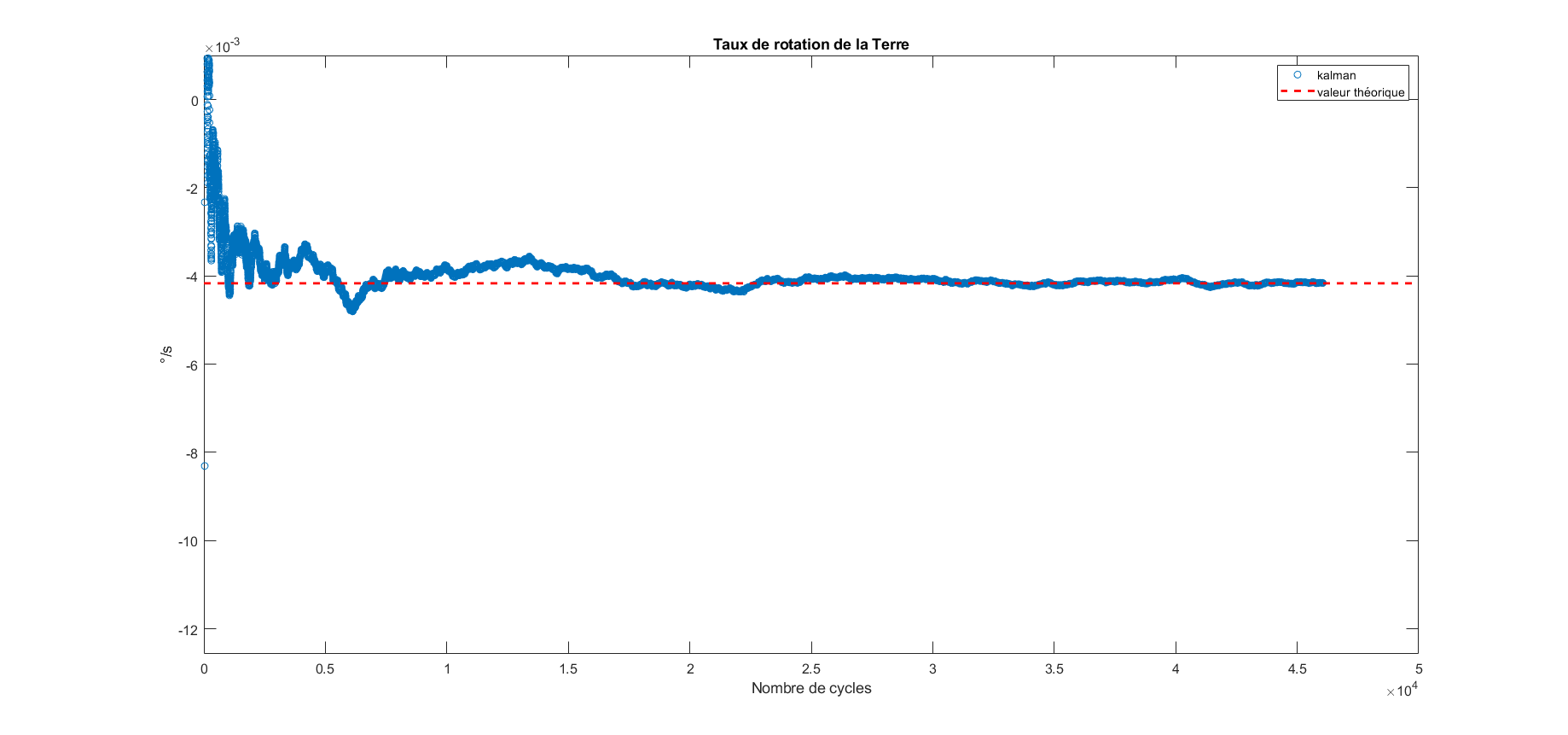
As shown in the video, the system works very well, with the correct value identified within 2 percent accuracy.

The attached figure illustrates, for one trial, the convergence of the Kalman filter (about 20,000 cycles, or roughly 20 minutes). It can be seen that the measured value is slightly lower than the theoretical expectation by a few percent. In fact, while analyzing these results, I realized the importance of precisely aligning the device with true north. This observation led me to begin developing a MEMS gyrocompass that leverages the measurement of the Earth’s rotation rate to determine the direction of north : https://hackaday.io/project/202955-no-more-compass-true-north-via-earth-s-rotation

In any case, these results show that local measurement of the Earth’s rotation is now accessible to anyone interested.

Not for commercial use – © Selva Systems – Contact for license