🧠 Operating principle:
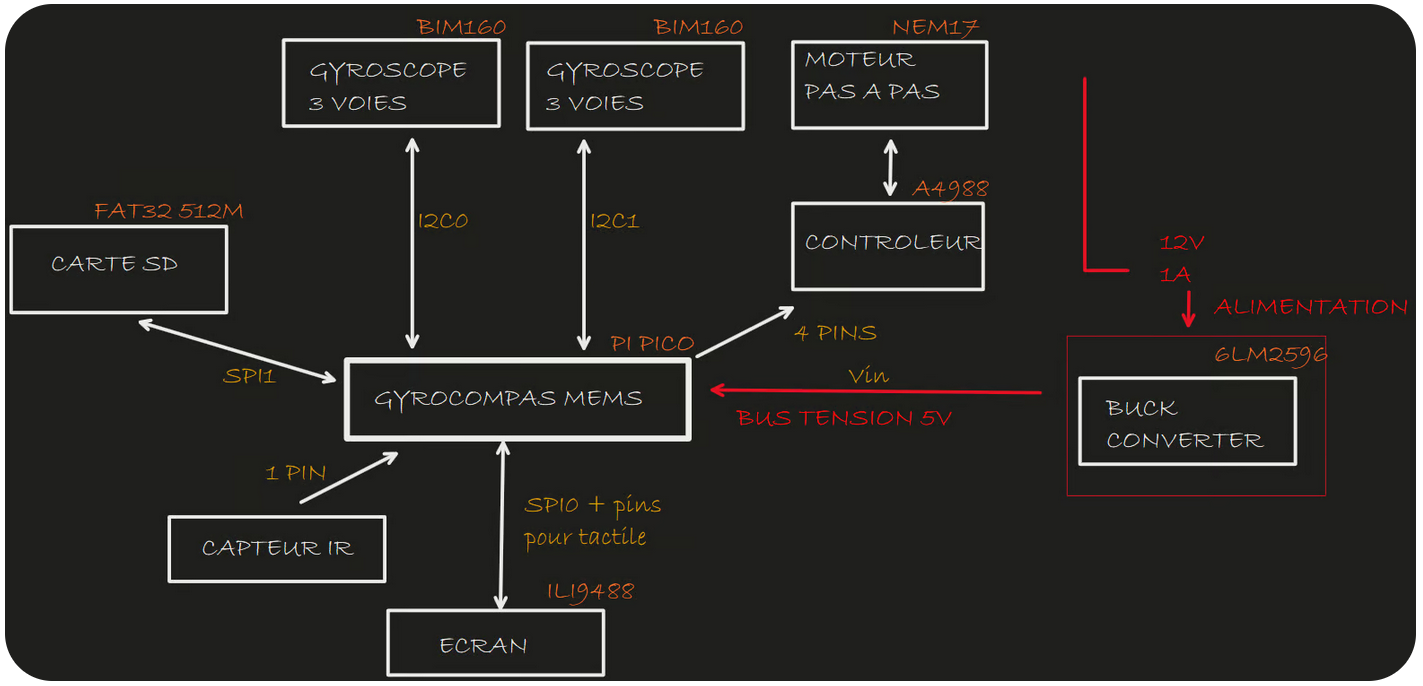
The prototype uses a Raspberry Pi Pico to run two BMI160 sensors mounted head-to-tail on a support driven by a NEMA-17 motor. By accumulating tens of thousands of measurements, It eliminates measurement bias through rapid reversal of the measurement direction. The use of dithering improves the resolution beyond the least significant bit (LSB). A five-state Kalman filter is applied at each position to estimate in real time the rotation rate along five directions in the horizontal plane. Finally, a cosine function is fitted to determine the latitude based on the amplitude, and the angle between the machine's reference frame and true north based on the phase shift.

🛠️ Hardware Architecture
The prototype is composed by the following components:
-
Microcontroller: Raspberry Pi Pico
-
Gyroscopes: Two BMI160 MEMS gyroscopes mounted in a head-to-tail configuration
-
Motion System: NEMA 17 stepper motor controlled by an A4988 driver
-
Indexing: Infrared endstop sensor for zero-position referencing
-
Display: 3.5″ SPI TFT screen for real-time data visualization
This setup enables precise measurement of Earth's rotation to determine true north and latitude without relying on magnetic fields
🎥 Project Demo
To see the system in action, check out the demonstration video below!
It shows how the device rotates through five directions, collects thousands of samples, and processes the data in real time to estimate true north and latitude — entirely without relying on any magnetic sensors.
The final result is displayed live on the onboard 3.5″ SPI screen (like a real compass).
Over longer periods (tens of minutes), the heading precision reaches about one degree.
However, what is truly impressive is that even after just a few complete cycles (a few thousand samples), the system already provides a remarkably good estimation of true north — as clearly visible in this video!
🔄 Measurement Cycle and Bias Cancellation
The system performs measurements according to the following cycle:
-
Stop at an azimuth θ and acquire 64 samples per gyroscope.
-
Rotate 180° (θ + π) and acquire a new set of samples.
-
Repeat this process for five azimuths, forming a complete cycle of about 12 seconds, followed by 2 seconds of processing.
🎯 Bias Suppression by Rapid Reversal
By measuring successively in two opposite directions, the system leverages the fact that gyroscope bias drifts slowly compared to the measurement time. Assuming Δt (≈ 0.5 s) is much shorter than the bias drift timescale (on the order of a minute), the horizontal component of Earth's rotation, ω_E,h, can be estimated as:
ω_E,h = 0.5 × (ω₁ − ω₂)
with
ω1 = +ω_E,h + b(t)
ω2 = -ω_E,h + b(t + Δt)
This technique, similar to the mode-reversal method used in certain MEMS gyroscopes, effectively cancels out the bias.
During the early tests, I applied exactly this method. However, in the approach developed here, a Kalman filter now fuses the measurements to estimate both the sensor bias and the rotation rate.
📈 Oversampling & Dithering: Beating the LSB
The BMI160 gyroscope has a resolution of 3.8 mdps per LSB at ±125 °/s full-scale range, whereas the Earth's rotation is 4,1667 mdps and horizontal component of Earth's rotation at 45° latitude is about 2,945 mdps. To detect such a faint signal, the system:
-
Leverages ambient noise (motor vibrations, electronic noise, quantization step) as a natural source of dithering.
-
Stacks tens of thousands of measurements over a few minutes.
With N = 10,000 samples, the quantization noise variance is reduced by a factor of 1 / sqrt(N)🧮 Real-time Kalman Filtering (5-state EKF)
The raw data from the two BMI160 gyroscopes are noisy (≈ 3.8 mdps/LSB) and subject to slow bias and temperature drift.
After each 12-second acquisition cycle (1,280 samples), the firmware runs a lightweight Kalman filter (~2 seconds processing time on the Pi Pico).1. State vector
For every azimuth θ, the filter tracks five variables:
-
ω : horizontal projection of Earth's rotation along θ
-
b_A : bias of gyro A
-
b_B : bias of gyro B
-
k_A * T : temperature drift (linear) of gyro A
-
k_B * T : temperature drift (linear) of gyro B
This 5-degree-of-freedom model whitens 1/f noise and temperature effects without burdening the Cortex-M0+.
2. Prediction model
Between the two half-turns (θ and θ + 180°), the system assumes:
-
Constant Earth rotation rate (ω)
-
Biases (b_A, b_B) and temperature effects drift slowly (modeled as random walk)
The process noise matrix (Q) is diagonal and tuned based on Allan variance measurements of the BMI160.
3. Measurement model
Each half-turn produces two signed measurements:
-
z_A = +ω + b_A + k_A * T + noise_A
-
z_B = -ω + b_B + k_B * T + noise_B
By combining z_A and z_B:
-
The bias terms largely cancel out
-
The system isolates ω (Earth rotation rate projected along the current azimuth)
The key: the two readings are taken only 0.5 seconds apart, making bias drift negligible compared to the Earth signal.
4. Update step
A standard Extended Kalman Filter (EKF) update is applied:
-
Compute Kalman gain
-
Correct the prediction based on new measurements
-
Update covariance
All matrices are small (5×5) and fit easily into the Pi Pico's RAM, ensuring fast real-time performance.
5. Outputs
-
The estimated ω(θ) at five azimuths are fitted to a cosine function:
-
Amplitude (A) gives the latitude.
-
Phase shift (θ₀) gives the angular misalignment between the device and true north.
-
-
Biases (b_A, b_B) are logged to monitor sensor health over time.
-
Temperature drift coefficients (k_A, k_B) can be used for open-loop compensation if needed.
Thanks to the EKF, the device achieves less than 1° heading error and around 1° latitude precision after about 20 minutes — using only 3€ sensors.
This level of accuracy would be impossible with simple averaging alone!
You can see more details on my website : https://selvasystems.net/innovations
In a future where magnetic north may wander — or even flip completely — traditional compasses will become unreliable. By relying only on Earth's immutable rotation, this MEMS-based gyrocompass offers a simple, mechanical way to find true north and latitude anywhere, anytime, without needing satellites, magnetic sensors, or external infrastructure. If the world goes dark, you'll still know where true north is - assuming electrow keeps delivering :)